- Joined
- 9/22/20
- Messages
- 6
- Points
- 13
European call
When solving the PDE for the value \(V\) of a European call option under the Black-Scholes model using a finite difference scheme, we have that
How to deduce the boundary conditions in a similar manner when solving the PDE for the value of a forward contract whose underlying follows the Schwartz mean reverting model? What I understand until now about forwards is
\[ \tag1 \frac{\partial F}{\partial t} + \alpha\Big(\mu-\lambda -\log S\Big)S\frac{\partial F}{\partial S}+\frac12\sigma^2S^2\frac{\partial^2F}{\partial S^2} = 0, \qquad \text{with }\lambda = \sigma\frac{\mu-r}\alpha \] whose solution is, letting \(\tau=T-t\)
\[ \tag2 F(S_t,\tau) = \mathbb E[S_t] = \exp\bigg(e^{-\alpha\tau}\log S_t +\Big(\mu-\frac{\sigma^2}{2\alpha}-\lambda\Big)(1-e^{-\alpha\tau})+\frac{\sigma^2}{4\alpha}(1-e^{-2\alpha\tau})\bigg) \]
Code
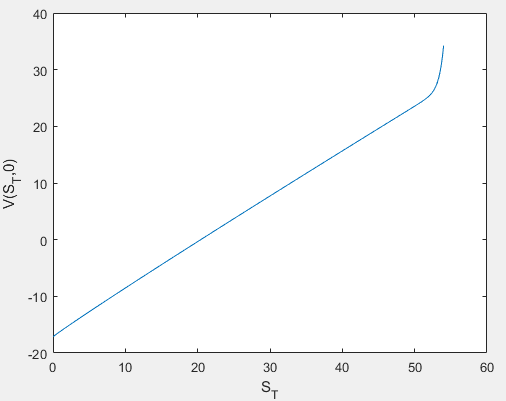
What follows is the Matlab code that computes the exact value of the option at time 0 (V_exact in the code) and the value approximated by the Euler explicit finite difference scheme (V_euler). The initial/terminal condition is applied at line 26 (F = ST), the next two lines are for the left end condition (F(1) = 0) and the right end condition (I don't know what to put here).
Moreover, I'm not sure that V_exact is computed correctly, should be \((F-K)\exp(-rT)\) or \(F-K\exp(-rT)\)?
When solving the PDE for the value \(V\) of a European call option under the Black-Scholes model using a finite difference scheme, we have that
- Initial/terminal condition. \(V(S_T,T) = \text{payoff}(S_T) = \max(S_T-K,0)\) (initial since the scheme is solved backward, terminal since it holds at the final time \(T\))
- Left end boundary condition. If \(S_0=0\) then \(S_t=0\) for all \(t\) and the option will surely be out of the money with payoff \(\max(0-K,0)=0\) and \(V(0,t)=0\) for all \(t\)
- Right end boundary condition. If \(S_0\) is large enough (w.r.t. to \(K\)) then \(S_t>K\) for all \(t\) and the option will end up in the money with payoff \(\max(S_t-K,0)=S_t-K\) and \(V(S_t,t)=S_t-Ke^{-r(T-t)}\) for all \(t\)
How to deduce the boundary conditions in a similar manner when solving the PDE for the value of a forward contract whose underlying follows the Schwartz mean reverting model? What I understand until now about forwards is
- There is no money exchanged when signing a forward contract so, using the notation below, I think that the value of the forward at time 0 is \(F(S_0,0)=0\)
- The payoff (of the option equivalent to this forward contract) is \(S_T-K\) since the holder is obliged to buy the underlying at expiry
\[ \tag1 \frac{\partial F}{\partial t} + \alpha\Big(\mu-\lambda -\log S\Big)S\frac{\partial F}{\partial S}+\frac12\sigma^2S^2\frac{\partial^2F}{\partial S^2} = 0, \qquad \text{with }\lambda = \sigma\frac{\mu-r}\alpha \] whose solution is, letting \(\tau=T-t\)
\[ \tag2 F(S_t,\tau) = \mathbb E[S_t] = \exp\bigg(e^{-\alpha\tau}\log S_t +\Big(\mu-\frac{\sigma^2}{2\alpha}-\lambda\Big)(1-e^{-\alpha\tau})+\frac{\sigma^2}{4\alpha}(1-e^{-2\alpha\tau})\bigg) \]
- Initial/terminal condition. Plugging \(\tau=0\) (ie \(t=T\)) in \((2)\) we get \(F(S_T,0) = \exp(\log S_T) = S_T\). This value appears also in the original paper by Schwartz (at page 5), so it is correct.
- Left end boundary condition. As in the European call case, if \(S_0=0\) then \(S_t=0\) for all \(t\) and from \((1)\) we get \(\dfrac{\partial F}{\partial t}=0\) ie \(F\) does not change in time, and since as said before \(F(S_0,0)=0\) (not sure though) it follows \(F(0,t)=0\) for all \(t\). But this means that the payoff of the option would be \(0-K\) that is negative, since prices cannot be negative how to deal with this fact?
- Right end boundary condition. If \(S_0\) is large enough (w.r.t. to \(K\)) then \(S_t>K\) for all \(t\) and the payoff of the option will be \(F(S_t,t)-K\) and \(V(S_t,t)=(F(S_t,t)-K)e^{-r(T-t)}\) for all \(t\), but what can we say about the value of \(F(S_t,t)\)?
Code
What follows is the Matlab code that computes the exact value of the option at time 0 (V_exact in the code) and the value approximated by the Euler explicit finite difference scheme (V_euler). The initial/terminal condition is applied at line 26 (F = ST), the next two lines are for the left end condition (F(1) = 0) and the right end condition (I don't know what to put here).
Moreover, I'm not sure that V_exact is computed correctly, should be \((F-K)\exp(-rT)\) or \(F-K\exp(-rT)\)?