Hello,
I have a question regarding the pricing and the hedging of options on Interest rates futures in Bloomberg. I don't really understand how the values are obtained by using the Normal model and the convention ( call on futures <=> put on the underlying).
Let's say I have an option on ERU3 Comdty:
Futures price = 99.583
strike = 100;
Time to expiry = 221 days
Implied volatility = 37.487 %;
risk Free rate = 0.398%
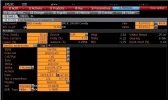
From bloomberg I have the following results (see the attached file):
price = 0.01
delta = 7.72%
gamma = 0.2054%
Vega = 2.62
Theta = - 0.22
Rho = -1.75
I am trying to get the same results from Matlab using the Black Model but it does not fit:
call = 0.4071;
put = 0;
delta = 0.97
And I could not find the right implied volatily by reversing the Black Model
Could someone explain carefully the formulae to use to obtain the right values?
I spent a lot of days on this issue..
Many thanks,
I have a question regarding the pricing and the hedging of options on Interest rates futures in Bloomberg. I don't really understand how the values are obtained by using the Normal model and the convention ( call on futures <=> put on the underlying).
Let's say I have an option on ERU3 Comdty:
Futures price = 99.583
strike = 100;
Time to expiry = 221 days
Implied volatility = 37.487 %;
risk Free rate = 0.398%
From bloomberg I have the following results (see the attached file):
price = 0.01
delta = 7.72%
gamma = 0.2054%
Vega = 2.62
Theta = - 0.22
Rho = -1.75
I am trying to get the same results from Matlab using the Black Model but it does not fit:
call = 0.4071;
put = 0;
delta = 0.97
And I could not find the right implied volatily by reversing the Black Model
Could someone explain carefully the formulae to use to obtain the right values?
I spent a lot of days on this issue..
Many thanks,