Hello,
sorry for stupid question, I'm a bit new to all this..
I want to check the distribution of rate of returns, on some Stock price. In text books, its always assumed that the rate of returns is Normally distributed (plz correct me if I'm wrong).
For a given Stock, if I build a histogram of x = (final_price -initial_price)/(initial_price)
shall I try to fit it with the Normal distribution? Shall I expect a good fit?
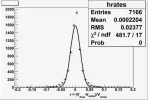
I took daily stock price of BAC and have built the histogram for rate of returns, for 7'166 days.
If I fit it with Normal distribution, Chi2 test gives me almost zero probability ...
(error at each bin = sqrt(bin content))
Any suggestions?
Thanks!
sorry for stupid question, I'm a bit new to all this..
I want to check the distribution of rate of returns, on some Stock price. In text books, its always assumed that the rate of returns is Normally distributed (plz correct me if I'm wrong).
For a given Stock, if I build a histogram of x = (final_price -initial_price)/(initial_price)
shall I try to fit it with the Normal distribution? Shall I expect a good fit?
I took daily stock price of BAC and have built the histogram for rate of returns, for 7'166 days.
If I fit it with Normal distribution, Chi2 test gives me almost zero probability ...
(error at each bin = sqrt(bin content))
Any suggestions?
Thanks!