- Joined
- 12/31/18
- Messages
- 1
- Points
- 11
Hi,
I read this interesting article: http://people.math.gatech.edu/~shenk/OptionsClub/kellyOptionTalk1.pdf
where a coin parlor game that pays 2x your bet when you win, and -1x has an optimal bet of 1/4 of your bank role. I tried replicating this with Python, but my results, don't match the theory.
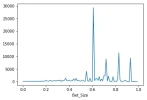
My approach is this. I test bet ratios from 0% to 99% of my bank roll. Then for each bet ratio, I generate N simulations, where for each simulation, I flip the coin N times. Below In my set up, heads is a win which pays 2x the bet, and tails is a loss which pays -1x the bet. According to the document above, the ideal bet is .25. My distrubtion say .6x.
Could someone see where my Python code is astray?

I read this interesting article: http://people.math.gatech.edu/~shenk/OptionsClub/kellyOptionTalk1.pdf
where a coin parlor game that pays 2x your bet when you win, and -1x has an optimal bet of 1/4 of your bank role. I tried replicating this with Python, but my results, don't match the theory.
My approach is this. I test bet ratios from 0% to 99% of my bank roll. Then for each bet ratio, I generate N simulations, where for each simulation, I flip the coin N times. Below In my set up, heads is a win which pays 2x the bet, and tails is a loss which pays -1x the bet. According to the document above, the ideal bet is .25. My distrubtion say .6x.
Could someone see where my Python code is astray?
import random
import matplotlib.pyplot as plt
import pandas as pd
#this program simulates a parlor coin game. You flip a coin N times. You always pick Heads. If you bet heads and win
#your return is 2x your bet. If you bet heads and lose, you lost your bet (not double your bet)
coin_value = ['H','T']
simulations = 100 #number of simulations of the N coin toss game
coin_tosses = 100 #number of times you flip a coin per simulation
game_result = []
for x in range(0,100): #i loop through bet percentages.
bet_size = (x/100) #set the bet percentage
for sim in range(0, simulations): #we run N simulations, which play N coin tosses per simulation
bank_roll = 100 #starting bank roll for each simulation
for coin_toss in range(0, coin_tosses): #we toss the coin N times
outcome = random.choice(coin_value)
if outcome == 'H': #if Heads, you win.
profit_loss = 2 * (bet_size * bank_roll) #Double your bet and add that to bankroll
result = 'W'
elif outcome == 'T': #if tails you lose.
profit_loss = -(bet_size * bank_roll) #Loss your bet and add that to bankroll
result = 'L'
bank_roll = bank_roll + profit_loss
#below I create a dataframe which has columns below
game_result.append([bet_size, result, bank_roll, sim, coin_toss])
df = pd.DataFrame(game_result, columns = ['Bet_Size','result','Bankroll', 'sim', 'coin_toss'])
df = df[df['coin_toss'] == (coin_tosses - 1)] #this selects the last coin toss for each simulation. Effectively, this
#is your ending balance after N coin tosses.
x = df.groupby(['Bet_Size'])['Bankroll'].mean() #calculated E[V] by bet size by averaging the simulations based on
#bet size