- Joined
- 12/25/20
- Messages
- 13
- Points
- 11
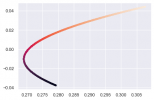
Hi all, could you please help me identify if there is anything wrong in my code? And if nothing is wrong, could you please let me know why the graph looks weird?
Efficient Frontier:
# -*- coding: utf-8 -*-
"""
Created on Wed Jan 13 17:03:13 2021
"""
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from math import *
from scipy.optimize import minimize
pd.set_option('display.max_rows', 10)
pd.set_option('display.max_columns', 10)
import pickle
from pandas_datareader import data as wb
tickers=['F','GM']
data=pd.DataFrame()
for t in tickers:
data[t]=wb.DataReader(t, data_source='yahoo', start='07-5-2012', end='5-7-2020')['Adj Close']
log_returns=np.log(data/data.shift(1))
num_ports=50000
ret_array=np.zeros(num_ports)
all_weights=np.zeros((num_ports, len(data.columns)))
vol_array=np.zeros(num_ports)
sharpe_array=np.zeros(num_ports)
for ind in range(num_ports):
weights=np.random.random(2)
weights=weights/np.sum(weights)
all_weights[ind,:]=weights
ret_array[ind]=np.sum(weights*log_returns.mean()*252)
vol_array[ind]=sqrt(np.dot(weights.T, np.dot(weights, log_returns.cov()*252)))
sharpe_array[ind]=ret_array[ind]/vol_array[ind]
plt.scatter(vol_array, ret_array, c=sharpe_array, s=8)
plt.show()