- Joined
- 5/2/06
- Messages
- 13,240
- Points
- 273
Bob,Wow, there is a serious lack of common sense prevailing in this thread.
You refer to the members' approach to the salary question, correct?
What is the common sense approach to it?
Bob,Wow, there is a serious lack of common sense prevailing in this thread.
@tylor
This isn't adequate enough.
Suppose instead of 100 dollars, the interviewer offered to double your net worth if you win or take you all your money if you lose. According to your logic, that is fair. However, no person would take that - a) because they're risk averse and b) the marginal utility of money decreases.
Wow, there is a serious lack of common sense prevailing in this thread.
@tylor
This isn't adequate enough.
Suppose instead of 100 dollars, the interviewer offered to double your net worth if you win or take you all your money if you lose. According to your logic, that is fair. However, no person would take that - a) because they're risk averse and b) the marginal utility of money decreases.
There's no way that the employer will pay more than £100... that's a certain (think 100%) loss for them all the time, lol!2) I flip a coin. If it's heads you pay me £100. What should I pay you to play this game? What about if I only have to get 1 heads in two tosses, what is the new price?
@AlexandreH
Let me refresh your memory with the question itself
There's no way that the employer will pay more than £100... that's a certain (think 100%) loss for them all the time, lol!
EDIT: I see what you are writing, and even under your interpretation (that is, employer:"how much do I have to pay if it's tails") you are not accounting for your risk-aversion.
OF COURSE NOBODY WILL PLAY ABOVE A CERTAIN PRICE. Why? Because of _risk aversion_.Consider the following game of chance: you pay a fixed fee to enter and then a fair coin is tossed repeatedly until a tail appears, ending the game. The pot starts at 1 dollar and is doubled every time a head appears. You win whatever is in the pot after the game ends. Thus you win 1 dollar if a tail appears on the first toss, 2 dollars if a head appears on the first toss and a tail on the second, 4 dollars if a head appears on the first two tosses and a tail on the third, 8 dollars if a head appears on the first three tosses and a tail on the fourth, etc. In short, you win 2<sup>k−1</sup> dollars if the coin is tossed k times until the first tail appears.
What would be a fair price to pay for entering the game? To answer this we need to consider what would be the average payout: With probability 1/2, you win 1 dollar; with probability 1/4 you win 2 dollars; with probability 1/8 you win 4 dollars etc. The expected value is thus
<dl><dd></dd></dl> <dl><dd> <dl><dd>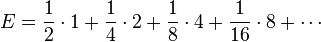 </dd></dl> </dd></dl> <dl><dd> <dl><dd>
</dd></dl> </dd></dl> <dl><dd> <dl><dd>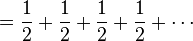 </dd></dl> </dd></dl> This sum diverges to infinity, and so the expected win for the player of this game, at least in its idealized form, in which the casino has unlimited resources, is an infinite amount of money. This means that the player should almost surely come out ahead in the long run, no matter how much he pays to enter; while a large payoff comes along very rarely, when it eventually does it will typically be far more than the amount of money that he has already paid to play. According to the usual treatment of deciding when it is advantageous and therefore rational to play, one should therefore play the game at any price if offered the opportunity.
</dd></dl> </dd></dl> This sum diverges to infinity, and so the expected win for the player of this game, at least in its idealized form, in which the casino has unlimited resources, is an infinite amount of money. This means that the player should almost surely come out ahead in the long run, no matter how much he pays to enter; while a large payoff comes along very rarely, when it eventually does it will typically be far more than the amount of money that he has already paid to play. According to the usual treatment of deciding when it is advantageous and therefore rational to play, one should therefore play the game at any price if offered the opportunity.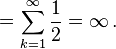
My note: Note that Bernoulli used u(w) = ln(w) because u'(w) = 1/w... the marginal utility is literally inversely proportional to the wealth. Risk aversion can logically be deducted from such a u(w).Expected utility theory
The classical resolution of the paradox involved the explicit introduction of a utility function, an expected utility hypothesis, and the presumption of diminishing marginal utility of money.
In Daniel Bernoulli's own words:
<dl><dd>The determination of the value of an item must not be based on the price, but rather on the utility it yields…. There is no doubt that a gain of one thousand ducats is more significant to the pauper than to a rich man though both gain the same amount.</dd></dl> A common utility model, suggested by Bernoulli himself, is the logarithmic function u(w) = ln(w) (known as “log utility”). It is a function of the gambler’s total wealth w, and the concept of diminishing marginal utility of money is built into it. By the expected utility hypothesis, expected utilities can be calculated the same way expected values are. For each possible event, the change in utility ln(wealth after the event) - ln(wealth before the event) will be weighted by the probability of that event occurring. Let c be the cost charged to enter the game. The expected utility of the lottery now converges to a finite value:
<dl><dd></dd></dl>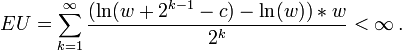
. It is what _you_ want the employer to pay. There is no "mathematically correct" answer (it depends on your utility function), but you should add a reasonable sum to your figures.You cannot account for risk aversion in problems like these. All you can do to answer this is run the calculations I have done and add that you are not accounting for risk-aversion.
I was illustrating a point... this is a Trading interview. You must absolutely talk about risk-aversion. It's too simple a concept to not mention it.
the use of equations below is mind boggling.
Oh really. So according to you, if I offer you 1x your money every 1 year you'd pick that because you get money sooner? But wait, 1x your money every 1 year means I don't have to increase your salary. Fantastic.
right. as if 2 x your salary every 2 years means increase in your salary LOL
according to the phrasing of the question, yes it does
according to the phrasing of the question, no it does not.
2 times your money every 2 years clearly means double your money every 2 years. and that's pretty much it. end of story.
you should definitely stay at the uni for a few more years. end of story.