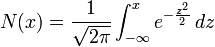Hello everyone,
I have been reading a great book about the mathematics that are used in asset pricing.
One of the famous quantitative tools that are used for pricing options is the Black Scholes PDE.
And the formula goes like this:
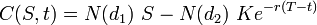
Where C(S,t) is the value of the call option,N(d1) is the delta for call on non-dividend paying asset and N(d2) the risk-neutral probability of the call option to expire in-the-money.
But most importantly,
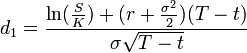
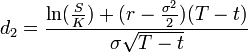
Here is where everything gets a little complicated...what are the formal names of d1 and d2? How were they computed/calculated? They are obviously solutions to some kind of differential equations but what are those?
Thank you!!!
I have been reading a great book about the mathematics that are used in asset pricing.
One of the famous quantitative tools that are used for pricing options is the Black Scholes PDE.
And the formula goes like this:
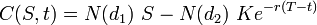
Where C(S,t) is the value of the call option,N(d1) is the delta for call on non-dividend paying asset and N(d2) the risk-neutral probability of the call option to expire in-the-money.
But most importantly,
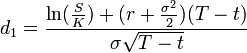
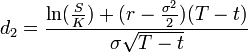
Here is where everything gets a little complicated...what are the formal names of d1 and d2? How were they computed/calculated? They are obviously solutions to some kind of differential equations but what are those?
Thank you!!!