Pre-Interview
(Ten minutes)
1) Mental Math: One million minus one hundred eleven.
2) Mental Math: Fifty-four percent of one hundred ten.
These have been solved above -- not much to add.
3) Game: With one die, suppose in a round, you earn the amount of dollars equal to the value of the upwards face of the die. (eg. you earn $6 if you roll a six.) Now also suppose after your first roll, you are given the opportunity to cancel your first and roll again, taking that value as the final value. What should your strategy be?
If you're only rolling once, then the expected value of the game is 3.5. So, if your first roll is a 1, 2, or 3, you should opt to roll again, and if you receive a 4, 5, or 6, then you should keep that value.
4) What's the closest integer to the square root of 1420.
Again, solved above.
5) You and a roommate are hosting a party. You invite 10 other pairs of roommates. During the party you poll everyone at the party (excluding yourself) and ask how many hands each person shook. Two conditions:
a) Each person did not shake his roommate's hand.
b) Each person shook a different number of hands.
Question: How many hands did you roommate shake?
There are 21 people to assign handshake numbers to; the maximum number of possible handshakes a single person could have made is 20, since a person can't shake hands with himself or his roommate. So, the 21 people have values from 0-20, inclusive. After trying this problem out with smaller cases, it should be clear that the sum of a pair of roommates' handshakes must equal 20. But this means that there must exist a pair of roommates with 10 handshakes each; you must be one of these roommates, since everybody shook a different number of peoples' hands. Therefore, your roommate shook 10 hands.
6) a) You roll a die, and are given an amount in dollar equal to the number on the die. What would you pay to play this game if you played it a lot of times?
This is a very unclear question; the expected value per roll is (1 + 6) / 2 = 3.5. So 3.5 * # of rolls allowed?
b) now say that when you roll the die, you're allowed to either take the money that you'd get with the roll, or roll a second time; if you roll a second time, you're obligated to take the number of dollars that you get with the second roll. Now what is the worth of the game?
It's easy to show that the optimal strategy must take the form "if current value <= T, then roll again; else, stay" -- to prove this, consider all possible other strategies and show that they must be inferior. Now, we just need to find T. On the first roll, the probability of getting <= T is T/6 and > T is 1-(T/6). In the latter case, the expected value is (6+T+1)/2. In the former case, the expected value is (1+6)/2 = 3.5, since we're forced to keep the second roll's value. The total expected value is T/6 * 3.5 + [1-(T/6)] * (T+7)/2. Maximizing with respect to T, we get T = 3. Substituting, the game value is $4.25.
c) Same thing as above, except you have an option to play the game a third time.
Too lazy to write it out; but this is the same thing as part b). I'm pretty sure that there's a nice way to do this if you have the option to play the game a total of n times via recursion.
Interview
(Thirty minutes)
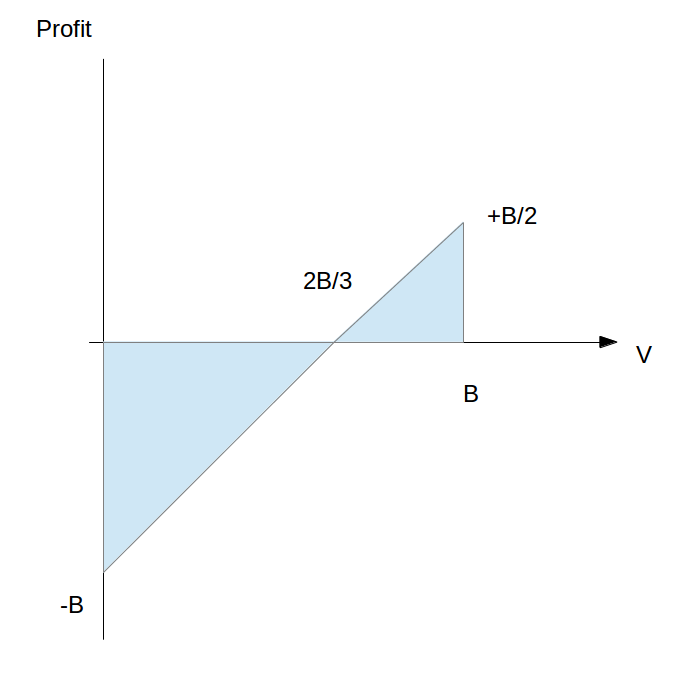
1) Suppose you are given the opportunity to bid for a treasure chest, which you know with 100% confidence to be priced anywhere between $0-$1000. If you bid equal to or above the price, you win the treasure chest (at the cost of your bid). If you bid below the price, you do not earn the treasure chest. Now, also suppose you have a friend who is willing to buy the treasure chest from you for one and a half times the price of the treasure chest (should you obtain the chest). What should your bid be?
I'm assuming that the probability distribution of the treasure chest is uniform; this makes sense if we assume no prior knowledge on the treasure chest. Suppose our bid is B and the price of the chest is C; note that B is a fixed value while C is a random variable. We have that P(C < B) = B/1000 and P(C >= B) = 1 - B/1000. In the latter case, our net gain is 0. In the former case, our net gain is 1.5C - B. Our expected net gain is thus E[B/1000 * (1.5C - B)] = B/1000 * (1.5*500-B) = B*(750-B)/1000. This is maximized when B = 375, so this is the right bid.
More generally, if we don't know that the price of the treasure chest is uniform, then the only thing we need to know is the expected value of the treasure chest to compute the optimum bid.
2) In Baseball, the batting average is the number of hits over the number of at bats. Player A has a greater batting average than Player B in the first half of the season and the second half of the season. Is it possible that Player B would have a higher batting average for the entire season?
Yes; season 1 -- A scores 1 hit on 1 ball, B scores 999 hits on 1000 balls. Season 2 -- A scores 10 hits on 20 balls, B scores 9 hits on 20 balls.
3) How much calories does a Big Mac have? Would you bet $1 on it? How about $10?
I guessed 900 calores; I wouldn't bet anything on this, since I don't eat McDonalds :P
4) How many tons does the ocean weigh?
I know the distance from Florida to California to be about 3000 miles -- this spans 3 timezones, so the circumference of the earth is ~24000 miles => R = 24000 / (2 * pi) ~ 4000 miles (I'm assuming that pi = 3 everywhere). This is about 6400 km (surprisingly, the true radius is 6378 km, which isn't too far off). Now, assume the depth of the oceans to be 4 miles, or 7 km at max, on average. The total volume is then 0.75 * 4*pi*R^2 * depth, assuming that the oceans cover 75% of the earth -- this is 3/4*4*3*(6400*6400)*7 ~ 9 * 8^4 * 7 * 10000 ~ 60 * 4000 * 10000 ~ 2 400 000 000 km^3 = 2.4 e 9 km^3 = 2.4 e 18 m^3. Ocean water has density 1 000 kg/m^3, so it's 2.4 e 21 kg in total. The actual weight is somewhere around 4 e 21 kg.
5) How much would you be willing to bet on it being within 25% of that at even odds?
I never came up with confidence intervals for the previous answer, but the trick to doing this is to come up with a confidence interval -- too lazy to do this now 
6) A company has a value V which is uniformly distributed between 0 and 1. you are planning to place a bid B for the company. If B is smaller than V, then your bid loses and you get nothing; if B is larger than V, you get to purchase the company at price B, and the company will end up being worth 1.5 * V. What price B should you bid to maximize your profit?
This problem is identical to problem 1. It's 0.375.
7) On a sheet of paper, you have 100 statements written down. the first says, "at most 0 of these 100 statements are true." the second says, "at most 1 of these 100 statements are true." ... the nth says, "at most (n-1) of these 100 statements are true. ... the 100th says, "at most 99 of these statements are true." how many of the statements are true?
More generally, suppose that we have n statements, and let statement k read "at most k of these n statements are true" for k = 0, 1, 2, ..., n - 1. Note that if statement k is true, then so are statements k + 1, k + 2, ..., n - 1. But, if statement k is true, then there must be at most k true statements while n - k statements are true. We have that n - k <= k, so k >= n / 2. In our case, n = 100, so k >= 50 (round up). If k = 50 (statements 50 - 99 are true), then everything checks out. If k = 51 (statements 49 - 99 are true), this doesn't work out, so exactly 50 statements are true.
8) You have two decks of cards: one has 13 reds and 13 blacks, and the other has 26 reds and 26 blacks. We play a game in which you select one of the two decks, and pick two cards from it; you win the game if you select two black cards. Which deck should you select to maximize your chances of winning? Try to do this problem in your head, without writing any calculations down.
It's 26 and 26. After picking the first black card, the chances of choosing another one goes down; you want to make this decrease as small as possible, so choosing the 26 and 26 deck works better. If this is hard to see, imagine if you had 1000 reds and 1000 blacks. P(black the first time) = 1/2 and P(black the second time) = very close to 1/2. With a 2/2 deck, P(black the first time) = 1/2 and P(black the second time) = 1/3. More cards = better here.
9) You have a deck of 52 cards, and you keep taking pairs of cards out of the deck. if a pair of cards are both red, then you win that pair; if a pair of cards are both black, then I win that pair; if a pair of cards has one red and one black, then it's discarded. If, after going through the whole deck, you have more pairs than I do, then you win $1, and if I have more pairs than you do, I win $1. What is the value of this game in the long run?
Seems to be 0 to me by symmetry.