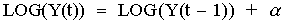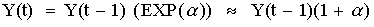Hi,
I've just been looking at random walk for discrete time and have a question. Using the formula to model the random walk:
S[i+1] = S * (1+μ*t + σ*φ*t^1/2)
where t = small increment of time
When I simulate this on a spreadsheet, with high volatility(σ), and relatively large timestep e.g. t=0.5, and drift (μ) = 0.15, I get negative asset price.
Looking at the formula, it is certainly possible to get negative asset price. e.g. timestep = 1, the drift is low, volatility is high enough to make the asset terms in the brackets a negative value.
Why is this so? I thought the model should not allow the modelled stock price to be negative?
regards,
I've just been looking at random walk for discrete time and have a question. Using the formula to model the random walk:
S[i+1] = S * (1+μ*t + σ*φ*t^1/2)
where t = small increment of time
When I simulate this on a spreadsheet, with high volatility(σ), and relatively large timestep e.g. t=0.5, and drift (μ) = 0.15, I get negative asset price.
Looking at the formula, it is certainly possible to get negative asset price. e.g. timestep = 1, the drift is low, volatility is high enough to make the asset terms in the brackets a negative value.
Why is this so? I thought the model should not allow the modelled stock price to be negative?
regards,